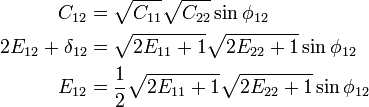Finite Strain Theory - Physical Interpretation of The Finite Strain Tensor

Physical Interpretation of The Finite Strain Tensor

The diagonal components of the Lagrangian finite strain tensor are related to the normal strain, e.g.

where is the normal strain or engineering strain in the direction .

The off-diagonal components of the Lagrangian finite strain tensor are related to shear strain, e.g.

where is the change in the angle between two line elements that were originally perpendicular with directions and, respectively.

Under certain circumstances, i.e. small displacements and small displacement rates, the components of the Lagrangian finite strain tensor may be approximated by the components of the infinitesimal strain tensor

Derivation of the physical interpretation of the Lagrangian and Eulerian finite strain tensors
The stretch ratio for the differential element (Figure) in the direction of the unit vector at the material point, in the undeformed configuration, is defined as

where is the deformed magnitude of the differential element .

Similarly, the stretch ratio for the differential element (Figure), in the direction of the unit vector at the material point, in the deformed configuration, is defined as

The square of the stretch ratio is defined as

Knowing that

we have

where and are unit vectors.

The normal strain or engineering strain in any direction can be expressed as a function of the stretch ratio,

Thus, the normal strain in the direction at the material point may be expressed in terms of the stretch ratio as

\begin{align} e_{(\mathbf I_1)}=\frac{dx_1-dX_1}{dX_1}&=\Lambda_{(\mathbf I_1)}-1\\ &=\sqrt {C_{11}} -1=\sqrt{\delta_{11}+2E_{11}}-1\\ &=\sqrt{1+2E_{11}}-1\end{align}\,\!

solving for we have

\begin{align} 2E_{11}&= \frac{(dx_1)^2 - (dX_1)^2}{(dX_1)^2} \\ E_{11}&= \left(\frac{dx_1-dX_1}{dX_1}\right)+ \frac {1}{2} \left(\frac{dx_1-dX_1}{dX_1}\right)^2 \\ &=e_{(\mathbf I_1)}+\frac{1}{2}e_{(\mathbf I_1)}^2\end{align}\,\!

The shear strain, or change in angle between two line elements and initially perpendicular, and oriented in the principal directions and, respectivelly, can also be expressed as a function of the stretch ratio. From the dot product between the deformed lines and we have

\begin{align} d\mathbf x_1 \cdot d\mathbf x_2&=dx_1dx_2\cos\theta_{12} \\ \mathbf F \cdot d\mathbf X_1\cdot \mathbf F\cdot d\mathbf X_2&= \sqrt {d\mathbf X_1 \cdot \mathbf F^T\cdot\mathbf F \cdot d\mathbf X_1}\cdot \sqrt {d\mathbf X_2 \cdot \mathbf F^T\cdot\mathbf F \cdot d\mathbf X_2} \cos\theta_{12} \\ \frac{d\mathbf X_1\cdot \mathbf F^T\cdot\mathbf F\cdot d\mathbf X_2}{dX_1dX_2}&=\frac{\sqrt {d\mathbf X_1 \cdot \mathbf F^T\cdot\mathbf F \cdot d\mathbf X_1}\cdot \sqrt {d\mathbf X_2 \cdot \mathbf F^T\cdot\mathbf F \cdot d\mathbf X_2}}{dX_1dX_2}\cos\theta_{12}\\ \mathbf I_1 \cdot \mathbf C \cdot \mathbf I_2&= \Lambda_{\mathbf I_1}\Lambda_{\mathbf I_2}\cos\theta_{12}\\ \end{align}\,\!

where is the angle between the lines and in the deformed configuration. Defining as the shear strain or reduction in the angle between two line elements that were originally perpendicular, we have

thus,

then

or

\begin{align} C_{12}&=\sqrt{C_{11}}\sqrt{C_{22}}\sin\phi_{12}\\ 2E_{12}+\delta_{12}&=\sqrt{2E_{11}+1}\sqrt{2E_{22}+1}\sin\phi_{12}\\ E_{12}&=\frac{1}{2}\sqrt{2E_{11}+1}\sqrt{2E_{22}+1}\sin\phi_{12}\end{align}\,\!

Read more about this topic:  Finite Strain Theory

Famous quotes containing the words physical, finite and/or strain:

    “Life on board a pleasure steamer violates every moral and physical condition of healthy life except fresh air.... It is a guzzling, lounging, gambling, dog’s life. The only alternative to excitement is irritability.”
    —George Bernard Shaw (1856–1950)

    “Sisters define their rivalry in terms of competition for the gold cup of parental love. It is never perceived as a cup which runneth over, rather a finite vessel from which the more one sister drinks, the less is left for the others.”
    —Elizabeth Fishel (20th century)

    “O Master, let me walk with Thee
    In lowly paths of service free;
    Tell me Thy secret, help me bear
    The strain of toil, the fret of care.”
    —Washington Gladden (1836–1918)