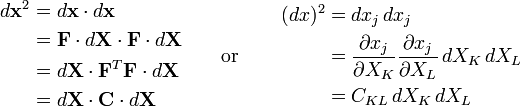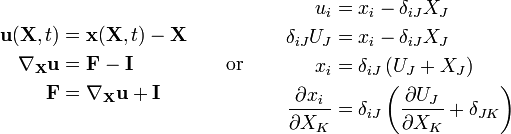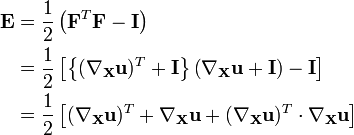Finite Strain Tensors
The concept of strain is used to evaluate how much a given displacement differs locally from a rigid body displacement (Ref. Lubliner). One of such strains for large deformations is the Lagrangian finite strain tensor, also called the Green-Lagrangian strain tensor or Green – St-Venant strain tensor, defined as
or as a function of the displacement gradient tensor
or
The Green-Lagrangian strain tensor is a measure of how much differs from . It can be shown that this tensor is a special case of a general formula for Lagrangian strain tensors (Hill 1968):
For different values of we have:
The Eulerian-Almansi finite strain tensor, referenced to the deformed configuration, i.e. Eulerian description, is defined as
or as a function of the displacement gradients we have
-
Derivation of the Lagrangian and Eulerain finite strain tensors A measure of deformation is the difference between the squares of the differential line element, in the undeformed configuration, and, in the deformed configuration (Figure 2). Deformation has occurred if the difference is non zero, otherwise a rigid-body displacement has occurred. Thus we have, In the Lagrangian description, using the material coordinates as the frame of reference, the linear transformation between the differential lines is
Then we have,
where are the components of the right Cauchy-Green deformation tensor, . Then, replacing this equation into the first equation we have,
or
where, are the components of a second-order tensor called the Green – St-Venant strain tensor or the Lagrangian finite strain tensor,
In the Eulerian description, using the spatial coordinates as the frame of reference, the linear transformation between the differential lines is
where are the components of the spatial deformation gradient tensor, . Thus we have
where the second order tensor is called Cauchy's deformation tensor, . Then we have,
or
where, are the components of a second-order tensor called the Eulerian-Almansi finite strain tensor,
Both the Lagrangian and Eulerian finite strain tensors can be conveniently expressed in terms of the displacement gradient tensor. For the Lagrangian strain tensor, first we differentiate the displacement vector with respect to the material coordinates to obtain the material displacement gradient tensor,
Replacing this equation into the expression for the Lagrangian finite strain tensor we have
or
Similarly, the Eulerian-Almansi finite strain tensor can be expressed as
Read more about this topic: Finite Strain Theory
Famous quotes containing the words finite and/or strain:
“Put shortly, these are the two views, then. One, that man is intrinsically good, spoilt by circumstance; and the other that he is intrinsically limited, but disciplined by order and tradition to something fairly decent. To the one party man’s nature is like a well, to the other like a bucket. The view which regards him like a well, a reservoir full of possibilities, I call the romantic; the one which regards him as a very finite and fixed creature, I call the classical.”
—Thomas Ernest Hulme (1883–1917)
“O Master, let me walk with thee
In lowly paths of service free;
Tell me thy secret; help me bear
The strain of toil, the fret of care;”
—Washington Gladden (1836–1918)