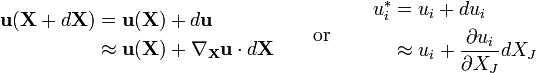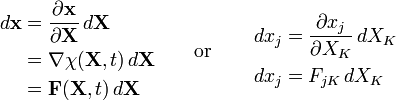Finite Strain Theory - Deformation Gradient Tensor

Deformation Gradient Tensor

Consider a particle or material point with position vector in the undeformed configuration (Figure 2). After a displacement of the body, the new position of the particle indicated by in the new configuration is given by the vector position . The coordinate systems for the undeformed and deformed configuration can be superimposed for convenience.

Consider now a material point neighboring, with position vector . In the deformed configuration this particle has a new position given by the position vector . Assuming that the line segments and joining the particles and in both the undeformed and deformed configuration, respectively, to be very small, then we can express them as and . Thus from Figure 2 we have

$\begin{align} \mathbf{x}+ d\mathbf{x}&= \mathbf{X}+d\mathbf{X}+\mathbf{u}(\mathbf{X}+d\mathbf{X}) \\ d\mathbf{x} &= \mathbf{X}-\mathbf{x}+d\mathbf{X}+\mathbf{u}(\mathbf{X}+d\mathbf{X}) \\ &= d\mathbf{X}+\mathbf{u}(\mathbf{X}+d\mathbf{X})-\mathbf{u}(\mathbf{X}) \\ &= d\mathbf{X}+d\mathbf{u} \\ \end{align} \,\!$

where is the relative displacement vector, which represents the relative displacement of with respect to in the deformed configuration.

For an infinitesimal element, and assuming continuity on the displacement field, it is possible to use a Taylor series expansion around point, neglecting higher-order terms, to approximate the components of the relative displacement vector for the neighboring particle as

$\begin{align} \mathbf{u}(\mathbf{X}+d\mathbf{X})&=\mathbf{u}(\mathbf{X})+d\mathbf{u}\\ &\approx \mathbf{u}(\mathbf{X})+\nabla_{\mathbf X}\mathbf u\cdot d\mathbf X \end{align} \qquad \text {or} \qquad \begin{align} u_i^* &= u_i+du_i\\ &\approx u_i+\frac{\partial u_i}{\partial X_J}dX_J\\ \end{align}\,\!$

Thus, the previous equation can be written as

$\begin{align} d\mathbf x&=d\mathbf X+d\mathbf u \\ &=d\mathbf X+\nabla_{\mathbf X}\mathbf u\cdot d\mathbf X\\ &=\left(\mathbf I + \nabla_{\mathbf X}\mathbf u\right)d\mathbf X\\ &=\mathbf F d\mathbf X \end{align} \,\!$

The material deformation gradient tensor is a second-order tensor that represents the gradient of the mapping function or functional relation, which describes the motion of a continuum. The material deformation gradient tensor characterizes the local deformation at a material point with position vector, i.e. deformation at neighbouring points, by transforming (linear transformation) a material line element emanating from that point from the reference configuration to the current or deformed configuration, assuming continuity in the mapping function, i.e. differentiable function of and time, which implies that cracks and voids do not open or close during the deformation. Thus we have,

$\begin{align} d\mathbf{x} &=\frac {\partial \mathbf{x}} {\partial \mathbf {X}}\,d\mathbf{X} \\ &= \nabla \chi(\mathbf X,t) \,d\mathbf{X} \\ &= \mathbf F(\mathbf X,t) \,d\mathbf{X} \\ \end{align} \qquad \text{or} \qquad \begin{align} dx_j&=\frac{\partial x_j}{\partial X_K}\,dX_K \\ dx_j&=F_{jK}\,dX_K \end{align}\,\!$

The deformation gradient tensor is related to both the reference and current configuration, as seen by the unit vectors and, therefore it is a two-point tensor.

Due to the assumption of continuity of, has the inverse, where is the spatial deformation gradient tensor. Then, by the implicit function theorem (Lubliner), the Jacobian determinant must be nonsingular, i.e.

Read more about this topic: Finite Strain Theory