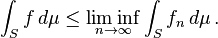Fatou's Lemma - Standard Statement of Fatou's Lemma

Standard Statement of Fatou's Lemma

Let f1, f2, f3, . . . be a sequence of non-negative measurable functions on a measure space (S,Σ,μ). Define the function f : S → a.e. pointwise limit by

f(s) =\liminf_{n\to\infty} f_n(s),\qquad s\in S.

Then f  is measurable and

\int_S f\,d\mu \le \liminf_{n\to\infty} \int_S f_n\,d\mu\,.

Note: The functions are allowed to attain the value +∞ and the integrals may also be infinite.

Read more about this topic:  Fatou's Lemma

Famous quotes containing the words standard and/or statement:

    “Where shall we look for standard English but to the words of a standard man?”
    —Henry David Thoreau (1817–1862)

    “Most personal correspondence of today consists of letters the first half of which are given over to an indexed statement of why the writer hasn’t written before, followed by one paragraph of small talk, with the remainder devoted to reasons why it is imperative that the letter be brought to a close.”
    —Robert Benchley (1889–1945)