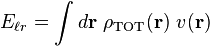Ewald Summation - Derivation

Derivation

Ewald summation rewrites the interaction potential as the sum of two terms

where represents the short-range term that sums quickly in real space and represents the long-range term that sums quickly in Fourier space. The long-ranged part should be finite for all arguments (most notably r = 0) but may have any convenient mathematical form, most typically a Gaussian distribution. The method assumes that the short-range part can be summed easily; hence, the problem becomes the summation of the long-range term. Due to the use of the Fourier sum, the method implicitly assumes that the system under study is infinitely periodic (a sensible assumption for the interiors of crystals). One repeating unit of this hypothetical periodic system is called a unit cell. One such cell is chosen as the "central cell" for reference and the remaining cells are called images.

The long-range interaction energy is the sum of interaction energies between the charges of a central unit cell and all the charges of the lattice. Hence, it can be represented as a double integral over two charge density fields representing the fields of the unit cell and the crystal lattice

$E_{\ell r} = \iint d\mathbf{r}\, d\mathbf{r}^\prime\, \rho_\text{TOT}(\mathbf{r}) \rho_{uc}(\mathbf{r}^\prime) \ \varphi_{\ell r}(\mathbf{r} - \mathbf{r}^\prime)$

where the unit-cell charge density field is a sum over the positions of the charges in the central unit cell

$\rho_{uc}(\mathbf{r}) \ \stackrel{\mathrm{def}}{=}\ \sum_{\mathrm{charges}\ k} q_k \delta(\mathbf{r} - \mathbf{r}_k)$

and the total charge density field is the same sum over the unit-cell charges and their periodic images

$\rho_\text{TOT}(\mathbf{r}) \ \stackrel{\mathrm{def}}{=}\ \sum_{n_1, n_2, n_3} \sum_{\mathrm{charges}\ k} q_k \delta(\mathbf{r} - \mathbf{r}_k - n_1 \mathbf{a}_1 - n_2 \mathbf{a}_2 - n_3 \mathbf{a}_3)$

Here, is the Dirac delta function, and are the lattice vectors and, and range over all integers. The total field can be represented as a convolution of with a lattice function

$L(\mathbf{r}) \ \stackrel{\mathrm{def}}{=}\ \sum_{n_1, n_2, n_3} \delta(\mathbf{r} - n_1 \mathbf{a}_{1} - n_{2} \mathbf{a}_2 - n_3 \mathbf{a}_3)$

Since this is a convolution, the Fourier transformation of is a product

$\tilde{\rho}_\text{TOT}(\mathbf{k}) = \tilde{L}(\mathbf{k}) \tilde{\rho}_{uc}(\mathbf{k})$

where the Fourier transform of the lattice function is another sum over delta functions

$\tilde{L}(\mathbf{k}) = \frac{\left(2\pi \right)^{3}}{\Omega} \sum_{m_1, m_2, m_3} \delta(\mathbf{k} - m_1 \mathbf{b}_1 - m_2 \mathbf{b}_2 - m_3 \mathbf{b}_3)$

where the reciprocal space vectors are defined (and cyclic permutations) where is the volume of the central unit cell (if it is geometrically a parallelepiped, which is often but not necessarily the case). Note that both and are real, even functions.

For brevity, define an effective single-particle potential

$v(\mathbf{r}) \ \stackrel{\mathrm{def}}{=}\ \int d\mathbf{r}^{\prime}\, \rho_{uc}(\mathbf{r}^\prime) \ \varphi_{\ell r}(\mathbf{r} - \mathbf{r}^\prime)$

Since this is also a convolution, the Fourier transformation of the same equation is a product

$\tilde{V}(\mathbf{k}) \ \stackrel{\mathrm{def}}{=}\ \tilde{\rho}_{uc}(\mathbf{k}) \tilde{\Phi}(\mathbf{k})$

where the Fourier transform is defined

$\tilde{V}(\mathbf{k}) = \int d\mathbf{r} \ v(\mathbf{r}) \ e^{-i\mathbf{k} \cdot \mathbf{r}}$

The energy can now be written as a single field integral

$E_{\ell r} = \int d\mathbf{r} \ \rho_\text{TOT}(\mathbf{r}) \ v(\mathbf{r})$

Using Parseval's theorem, the energy can also be summed in Fourier space

$E_{\ell r} = \int \frac{d\mathbf{k}}{\left(2\pi\right)^3} \ \tilde{\rho}_\text{TOT}^*(\mathbf{k}) \tilde{V}(\mathbf{k}) = \int \frac{d\mathbf{k}}{\left(2\pi\right)^3} \tilde{L}^*(\mathbf{k}) \left| \tilde{\rho}_{uc}(\mathbf{k})\right|^2 \tilde{\Phi}(\mathbf{k}) = \frac{1}{\Omega} \sum_{m_1, m_2, m_3} \left| \tilde{\rho}_{uc}(\mathbf{k})\right|^2 \tilde{\Phi}(\mathbf{k})$

where in the final summation.

This is the essential result. Once is calculated, the summation/integration over is straightforward and should converge quickly. The most common reason for lack of convergence is a poorly defined unit cell, which must be charge neutral to avoid infinite sums.

Read more about this topic: Ewald Summation