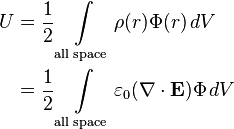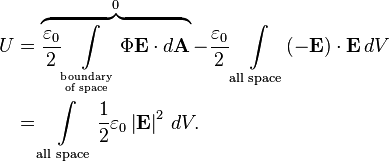Electric Potential Energy - Energy Stored in An Electrostatic Field Distribution

Energy Stored in An Electrostatic Field Distribution

The energy density, or energy per unit volume, of the electrostatic field of a continuous charge distribution is:

Outline of proof

One may take the equation for the electrostatic potential energy of a continuous charge distribution and put it in terms of the electrostatic field.

Since Gauss' law for electrostatic field in differential form states

where

  • is the electric field vector
  • is the total charge density including dipole charges bound in a material
  • is the permittivity of free space,

then,

\begin{align} U & = \frac{1}{2}\int \limits_{\text{all space}} \rho(r) \Phi(r) \, dV \\ & = \frac{1}{2}\int \limits_{\text{all space}} \varepsilon_0(\mathbf{\nabla}\cdot{\mathbf{E}})\Phi \, dV \end{align}

so, now using the following divergence vector identity

we have

using the divergence theorem and taking the area to be at infinity where

\begin{align} U & = \overbrace{\frac{\varepsilon_0}{2}\int\limits_{{}^\text{boundary}_\text{ of space}} \Phi\mathbf{E}\cdot d\mathbf A}^{0} - \frac{\varepsilon_0}{2}\int \limits_{\text{all space}} (-\mathbf{E})\cdot\mathbf{E} \, dV \\ & = \int \limits_{\text{all space}} \frac{1}{2}\varepsilon_0\left|{\mathbf{E}}\right|^2 \, dV. \end{align}

So, the energy density, or energy per unit volume of the electrostatic field is:

Read more about this topic:  Electric Potential Energy

Famous quotes containing the words energy, stored, field and/or distribution:

    “Children are intensely invested in getting their way. They will devote more emotional and intellectual energy to winning arguments than parents ever will, and are almost always better rested.”
    —Jean Callahan (20th century)

    “Health can be squandered, but not stored up.”
    —Mason Cooley (b. 1927)

    “The head must bow, and the back will have to bend,
    Wherever the darkey may go;
    A few more days, and the trouble all will end,
    In the field where the sugar-canes grow.
    A few more days for to tote the weary load,—
    No matter, ‘t will never be light;
    A few more days till we totter on the road:—
    Then my old Kentucky home, good-night!”
    —Stephen Collins Foster (1826–1884)

    “Classical and romantic: private language of a family quarrel, a dead dispute over the distribution of emphasis between man and nature.”
    —Cyril Connolly (1903–1974)