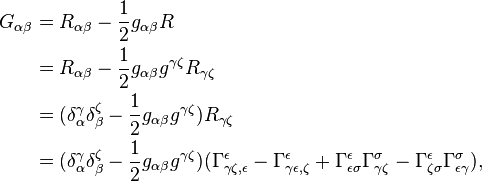Einstein Tensor - Explicit Form

Explicit Form

The Ricci tensor depends only on the metric tensor, so the Einstein tensor can be defined directly with just the metric tensor. However, this expression is complex and rarely quoted in textbooks. The complexity of this expression can be shown using the formula for the Ricci tensor in terms of Christoffel symbols:

\begin{align} G_{\alpha\beta} &= R_{\alpha\beta} - \frac{1}{2} g_{\alpha\beta} R \\ &= R_{\alpha\beta} - \frac{1}{2} g_{\alpha\beta} g^{\gamma\zeta} R_{\gamma\zeta} \\ &= (\delta^\gamma_\alpha \delta^\zeta_\beta - \frac{1}{2} g_{\alpha\beta}g^{\gamma\zeta}) R_{\gamma\zeta} \\ &= (\delta^\gamma_\alpha \delta^\zeta_\beta - \frac{1}{2} g_{\alpha\beta}g^{\gamma\zeta})(\Gamma^\epsilon_{\gamma\zeta,\epsilon} - \Gamma^\epsilon_{\gamma\epsilon,\zeta} + \Gamma^\epsilon_{\epsilon\sigma} \Gamma^\sigma_{\gamma\zeta} - \Gamma^\epsilon_{\zeta\sigma} \Gamma^\sigma_{\epsilon\gamma}), \end{align}

where is the Kronecker tensor and the Christoffel symbol is defined as

Before cancellations, this formula results in individual terms. Cancellations bring this number down somewhat.

In the special case of a locally inertial reference frame near a point, the first derivatives of the metric tensor vanish and the component form of the Einstein tensor is considerably simplified:

where square brackets conventionally denote antisymmetrization over bracketed indices, i.e.

Read more about this topic:  Einstein Tensor

Famous quotes containing the words explicit and/or form:

    “... the Ovarian Theory of Literature, or, rather, its complement, the Testicular Theory. A recent camp follower ... of this explicit theory is ... Norman Mailer, who has attributed his own gift, and the literary gift in general, solely and directly to the possession of a specific pair of organs. One writes with these organs, Mailer has said ... and I have always wondered with what shade of ink he manages to do it.”
    —Cynthia Ozick (b. 1928)

    “I find in most novels no imagination at all. They seem to think the highest form of the novel is to write about marriage, because that’s the most important thing there is for middle-class people.”
    —Gore Vidal (b. 1925)