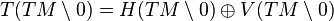Double Tangent Bundle - Nonlinear Covariant Derivatives On Smooth Manifolds

Nonlinear Covariant Derivatives On Smooth Manifolds

The canonical flip makes it possible to define nonlinear covariant derivatives on smooth manifolds as follows. Let

T(TM\setminus 0) = H(TM\setminus 0) \oplus V(TM\setminus 0)

be an Ehresmann connection on the slit tangent bundle TM/0 and consider the mapping

D:(TM\setminus 0)\times \Gamma(TM) \to TM; \quad D_XY := (\kappa\circ j)(Y_*X),

where Y*:TM→TTM is the push-forward, j:TTM→TTM is the canonical flip and κ:T(TM/0)→TM/0 is the connector map. The mapping DX is a derivation in the module Γ (TM) of smooth vector fields on M in the sense that

  • .
  • .

Any mapping DX with these properties is called a (nonlinear) covariant derivative on M. The term nonlinear refers to the fact that this kind of covariant derivative DX on is not necessarily linear with respect to the direction X∈TM/0 of the differentiation.

Looking at the local representations one can confirm that the Ehresmann connections on (TM/0,πTM/0,M) and nonlinear covariant derivatives on M are in one-to-one correspondence. Furthermore, if DX is linear in X, then the Ehresmann connection is linear in the secondary vector bundle structure, and DX coincides with its linear covariant derivative if and only if the torsion of the connection vanishes.

Read more about this topic:  Double Tangent Bundle

Famous quotes containing the word smooth:

    “It may seem strange that any road through such a wilderness should be passable, even in winter, when the snow is three or four feet deep, but at that season, wherever lumbering operations are actively carried on, teams are continually passing on the single track, and it becomes as smooth almost as a railway.”
    —Henry David Thoreau (1817–1862)