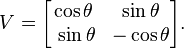Dilation (operator Theory) - Applications

Applications

We can show that every contraction on Hilbert spaces has a unitary dilation. A possible construction of this dilation is as follows. For a contraction T, the operator

is positive, where the continuous functional calculus is used to define the square root. The operator D_T is called the defect operator of T. Let V be the operator on

defined by the matrix

V is clearly a dilation of T. Also, T(I - T*T) = (I - TT*)T implies

Using this one can show, by calculating directly, that V is unitary, therefore an unitary dilation of T. This operator V is sometimes called the Julia operator of T.

Notice that when T is a real scalar, say, we have

which is just the unitary matrix describing rotation by θ. For this reason, the Julia operator V(T) is sometimes called the elementary rotation of T.

We note here that in the above discussion we have not required the calculus property for a dilation. Indeed, direct calculation shows the Julia operator fails to be a "degree-2" dilation in general, i.e. it need not be true that

.

However, it can also be shown that any contraction has a unitary dilation which does have the calculus property above. This is Sz.-Nagy's dilation theorem. More generally, if is a Dirichlet algebra, any operator T with as a spectral set will have a normal dilation with this property. This generalises Sz.-Nagy's dilation theorem as all contractions have the unit disc as a spectral set.