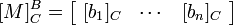Coordinate Vector - Basis Transformation Matrix

Basis Transformation Matrix

Let B and C be two different bases of a vector space V, and let us mark with the matrix which has columns consisting of the C representation of basis vectors b1, b2, ..., bn:

_{C}^{B} = \begin{bmatrix} \ _C & \cdots & _C \ \end{bmatrix}

This matrix is referred to as the basis transformation matrix from B to C, and can be used for transforming any vector v from a B representation to a C representation, according to the following theorem:

If E is the standard basis, the transformation from B to E can be represented with the following simplified notation:

where

and

Read more about this topic:  Coordinate Vector

Famous quotes containing the words basis and/or matrix:

    “Even upon such a basis hast thou built
    A monument, whose cement hath been guilt!”
    —George Gordon Noel Byron (1788–1824)

    “In all cultures, the family imprints its members with selfhood. Human experience of identity has two elements; a sense of belonging and a sense of being separate. The laboratory in which these ingredients are mixed and dispensed is the family, the matrix of identity.”
    —Salvador Minuchin (20th century)