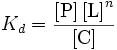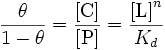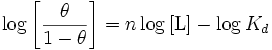Cooperative Binding - The Hill Coefficient

The Hill Coefficient

The Hill coefficient provides a quantitative method for characterizing binding cooperativity. The macromolecule is assumed to bind to ligands simultaneously (where is to be determined)

\mathrm{P} + n\mathrm{L} \leftrightarrow \mathrm{C}

to form the complex C. Hence the dissociation constant equals

K_{d} = \frac{\left\left^{n}}{\left}

Let the variable represent the fraction of binding sites that are occupied on the macromolecule. Then, represents the fraction of binding sites that are not occupied, giving the ratio

\frac{\theta}{1 -\theta} = \frac{\left}{\left} = \frac{\left^{n}}{K_{d}}

Taking the logarithm yields an equation linear in

\log \left = n \log \left - \log K_{d}

Hence, the slope of this line yields, whereas its intercept is determined by .

More generally, plotting versus and taking the slope gives the effective number of ligands that are binding cooperatively at a particular ligand concentration . In a non-cooperative system such as myoglobin, the plot is a straight line with slope at all ligand concentrations. By contrast, in a system with positive cooperativity such as hemoglobin, the plot begins as a line with slope, then ramps up to a new line (also with slope ) that is offset upwards. The degree of cooperativity is characterized by the maximum slope in the "ramping up" region, which is ~2.8 for hemoglobin; thus, at its most cooperative, hemoglobin effectively binds three ligands in concert. The "ramping up" corresponds to an increase in the affinity (decrease in ) that occurs as the amount of bound ligand increases. Such plots are sometimes characterized as "sigmoid" due to their subtle "S"-shape.

Read more about this topic:  Cooperative Binding

Famous quotes containing the word hill:

    “The fact that Romans once inhabited her reflects no little dignity on Nature herself; that from some particular hill the Roman once looked out on the sea.”
    —Henry David Thoreau (1817–1862)