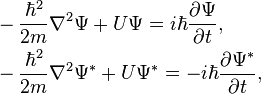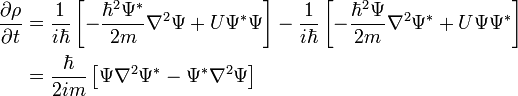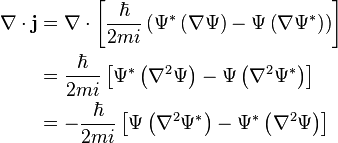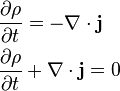Continuity Equation - Quantum Mechanics

Quantum Mechanics

In quantum mechanics, the conservation of probability also yields a continuity equation. The terms in the equation require these definitions, and are slightly less obvious than the other forms of volume densities, currents, current densities etc., so they are outlined here:

  • The wavefunction Ψ for a single particle in the position-time space (rather than momentum space) - i.e. functions of position r and time t, Ψ = Ψ(r, t) = Ψ(x, y, z, t).
  • The probability density function ρ = ρ(r, t) is:
  • The probability that a measurement of the particle's position will yield a value within V at t, denoted by P = Pr ∈ V(t), is:
  • The probability current (aka probability flux) j:

With these definitions the continuity equation reads:

Either form is usually quoted. Intuitively; the above quantities indicate this represents the flow of probability. The chance of finding the particle at some r t flows like a fluid, the particle itself does not flow deterministically in the same vector field.

Consistency with Schrödinger's equation
For this derivation see for example. The 3-d time dependent Schrödinger equation and its complex conjugate (i → –i) throughout are respectively:
\begin{align} & -\frac{\hbar^2}{2m}\nabla^2 \Psi + U\Psi = i\hbar \frac{\partial \Psi}{\partial t}, \\ & - \frac{\hbar^2}{2m}\nabla^2 \Psi^{*} + U\Psi^{*} = - i\hbar \frac{\partial \Psi^{*}}{\partial t} ,\\ \end{align}

where U is the potential function. The partial derivative of ρ with respect to t is:

Multiplying the Schrödinger equation by Ψ* then solving for, and similarly multiplying the complex conjugated Schrödinger equation by Ψ then solving for ;

\begin{align} & \Psi^*\frac{\partial \Psi}{\partial t} = \frac{1}{i\hbar } \left, \\ & \Psi \frac{\partial \Psi^*}{\partial t} = - \frac{1}{i\hbar } \left ,\\ \end{align}

substituting into the time derivative of ρ:

\begin{align} \frac{\partial \rho}{\partial t} & = \frac{1}{i\hbar } \left - \frac{1}{i\hbar } \left \\ & = \frac{\hbar}{2im} \left \\ \end{align}

The Laplacian operators (∇2) in the above result suggest that the right hand side is the divergence of j, and the reversed order of terms imply this is the negative of j, altogether:

\begin{align} \nabla \cdot \mathbf{j} & = \nabla \cdot \left \\ & = \frac{\hbar}{2mi} \left \\ & = - \frac{\hbar}{2mi} \left \\ \end{align}

so the continuity equation is:

\begin{align} & \frac{\partial \rho}{\partial t} = - \nabla \cdot \mathbf{j} \\ & \frac{\partial \rho}{\partial t} + \nabla \cdot \mathbf{j} = 0 \\ \end{align}

The integral form follows as for the general equation.

Read more about this topic:  Continuity Equation

Famous quotes containing the words quantum and/or mechanics:

    “The receipt to make a speaker, and an applauded one too, is short and easy.—Take of common sense quantum sufficit, add a little application to the rules and orders of the House, throw obvious thoughts in a new light, and make up the whole with a large quantity of purity, correctness, and elegancy of style.”
    —Philip Dormer Stanhope, 4th Earl Chesterfield (1694–1773)

    “It is only the impossible that is possible for God. He has given over the possible to the mechanics of matter and the autonomy of his creatures.”
    —Simone Weil (1909–1943)