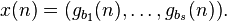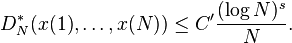Constructions of Low-discrepancy Sequences - The Halton Sequence

The Halton Sequence

The Halton sequence is a natural generalization of the van der Corput sequence to higher dimensions. Let s be an arbitrary dimension and b1, ..., bs be arbitrary coprime integers greater than 1. Define

x(n)=(g_{b_1}(n),\dots,g_{b_s}(n)).

Then there is a constant C depending only on b1, ..., bs, such that sequence {x(n)}n≥1 is a s-dimensional sequence with

D^*_N(x(1),\dots,x(N))\leq C'\frac{(\log N)^s}{N}.

Read more about this topic:  Constructions Of Low-discrepancy Sequences

Famous quotes containing the word sequence:

    “It isn’t that you subordinate your ideas to the force of the facts in autobiography but that you construct a sequence of stories to bind up the facts with a persuasive hypothesis that unravels your history’s meaning.”
    —Philip Roth (b. 1933)