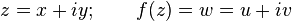Complex Plane - Notational Conventions

Notational Conventions

In complex analysis the complex numbers are customarily represented by the symbol z, which can be separated into its real (x) and imaginary (y) parts, like this:

z = x + iy\,

for example: z = 4 + 5i,

where x and y are real numbers, and i is the imaginary unit. In this customary notation the complex number z corresponds to the point (x, y) in the Cartesian plane.

In the Cartesian plane the point (x, y) can also be represented in polar coordinates as

(x, y) = (r\cos\theta, r\sin\theta)\qquad(r, \theta) = \left(\sqrt{x^2+y^2}, \quad \arctan\frac{y}{x}\right).\,

In the Cartesian plane it may be assumed that the arctangent takes values from −π/2 to π/2 (in radians), and some care must be taken to define the real arctangent function for points (x, y) when x ≤ 0. In the complex plane these polar coordinates take the form

z = x + iy = |z|\left(\cos\theta + i\sin\theta\right) = |z|e^{i\theta}\,

where

|z| = \sqrt{x^2+y^2}; \quad \theta = \arg(z) = \frac{1}{i}\ln\frac{z}{|z|} = -i\ln\frac{z}{|z|}.\,

Here |z| is the absolute value or modulus of the complex number z; θ, the argument of z, is usually taken on the interval 0 ≤ θ < 2π; and the last equality (to |z|eiθ) is taken from Euler's formula. Notice that the argument of z is multi-valued, because the complex exponential function is periodic, with period 2πi. Thus, if θ is one value of arg(z), the other values are given by arg(z) = θ + 2nπ, where n is any integer ≠ 0. While seldom used explicitly, the geometric view of the complex numbers is implicitly based on its structure of a Euclidean vector space of dimension 2, where the inner product of complex numbers w and z is given by ; then for a complex number z its absolute value |z| coincides with its Euclidean norm, and its argument arg(z) with the angle turning from 1 to z.

The theory of contour integration comprises a major part of complex analysis. In this context the direction of travel around a closed curve is important – reversing the direction in which the curve is traversed multiplies the value of the integral by −1. By convention the positive direction is counterclockwise. For example, the unit circle is traversed in the positive direction when we start at the point z = 1, then travel up and to the left through the point z = i, then down and to the left through −1, then down and to the right through −i, and finally up and to the right to z = 1, where we started.

Almost all of complex analysis is concerned with complex functions – that is, with functions that map some subset of the complex plane into some other (possibly overlapping, or even identical) subset of the complex plane. Here it is customary to speak of the domain of f(z) as lying in the z-plane, while referring to the range or image of f(z) as a set of points in the w-plane. In symbols we write

z = x + iy;\qquad f(z) = w = u + iv\,

and often think of the function f as a transformation of the z-plane (with coordinates (x, y)) into the w-plane (with coordinates (u, v)).

Read more about this topic:  Complex Plane

Famous quotes containing the word conventions:

    “Art, it seems to me, should simplify. That, indeed, is very nearly the whole of the higher artistic process; finding what conventions of form and what detail one can do without and yet preserve the spirit of the whole—so that all that one has suppressed and cut away is there to the reader’s consciousness as much as if it were in type on the page.”
    —Willa Cather (1873–1947)