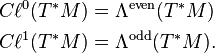Clifford Bundle - Clifford Bundle of A Riemannian Manifold

Clifford Bundle of A Riemannian Manifold

If M is a Riemannian manifold with metric g, then the Clifford bundle of M is the Clifford bundle generated by the tangent bundle TM. One can also build a Clifford bundle out of the cotangent bundle T*M. The metric induces a natural isomorphism TM = T*M and therefore an isomorphism Cℓ(TM) = Cℓ(T*M).

There is a natural vector bundle isomorphism between the Clifford bundle of M and the exterior bundle of M:

This is an isomorphism of vector bundles not algebra bundles. The isomorphism is induced from the corresponding isomorphism on each fiber. In this way one can think of sections of the Clifford bundle as differential forms on M equipped with Clifford multiplication rather than the wedge product (which is independent of the metric).

The above isomorphism respects the grading in the sense that

\begin{align} C\ell^0(T^*M) &= \Lambda^{\mathrm{even}}(T^*M)\\ C\ell^1(T^*M) &= \Lambda^{\mathrm{odd}}(T^*M). \end{align}

Read more about this topic:  Clifford Bundle

Famous quotes containing the words clifford, bundle and/or manifold:

    “Youth is not a question of years: one is young or old from birth.”
    —Natalie Clifford Barney (1876–1972)

    ““There is Lowell, who’s striving Parnassus to climb
    With a whole bale of isms tied together with rhyme,
    He might get on alone, spite of brambles and boulders,
    But he can’t with that bundle he has on his shoulders,
    The top of the hill he will ne’er come nigh reaching
    Till he learns the distinction ‘twixt singing and preaching;”
    —James Russell Lowell (1819–1891)

    “They had met, and included in their meeting the thrust of the manifold grass stems, the cry of the peewit, the wheel of the stars.”
    —D.H. (David Herbert)