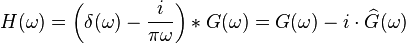Causal Filter - Characterization of Causal Filters in The Frequency Domain

Characterization of Causal Filters in The Frequency Domain

Let h(t) be a causal filter with corresponding Fourier transform H(ω). Define the function

g(t) = {h(t) + h^{*}(-t) \over 2}

which is non-causal. On the other hand, g(t) is Hermitian and, consequently, its Fourier transform G(ω) is real-valued. We now have the following relation

h(t) = 2\, \Theta(t) \cdot g(t)\,

where Θ(t) is the Heaviside unit step function.

This means that the Fourier transforms of h(t) and g(t) are related as follows

H(\omega) = \left(\delta(\omega) - {i \over \pi \omega}\right) * G(\omega) = G(\omega) - i\cdot \widehat G(\omega) \,

where is a Hilbert transform done in the frequency domain (rather than the time domain). The sign of may depend on the definition of the Fourier Transform.

Taking the Hilbert transform of the above equation yields this relation between "H" and its Hilbert transform:

\widehat H(\omega) = i H(\omega)

Read more about this topic:  Causal Filter

Famous quotes containing the words causal, filters, frequency and/or domain:

    “There is the illusion of time, which is very deep; who has disposed of it? Mor come to the conviction that what seems the succession of thought is only the distribution of wholes into causal series.”
    —Ralph Waldo Emerson (1803–1882)

    “Raise a million filters and the rain will not be clean, until the longing for it be refined in deep confession. And still we hear, If only this nation had a soul, or, Let us change the way we trade, or, Let us be proud of our region.”
    —Leonard Cohen (b. 1934)

    “The frequency of personal questions grows in direct proportion to your increasing girth. . . . No one would ask a man such a personally invasive question as “Is your wife having natural childbirth or is she planning to be knocked out?” But someone might ask that of you. No matter how much you wish for privacy, your pregnancy is a public event to which everyone feels invited.”
    —Jean Marzollo (20th century)

    “In the domain of Political Economy, free scientific inquiry meets not merely the same enemies as in all other domains. The peculiar nature of the material it deals with, summons as foes into the field of battle the most violent, mean and malignant passions of the human breast, the Furies of private interest.”
    —Karl Marx (1818–1883)