The Difference of Gaussians Approach
From the fact that the scale space representation satisfies the diffusion equation
it follows that the Laplacian of the Gaussian operator can also be computed as the limit case of the difference between two Gaussian smoothed images (scale space representations)
.
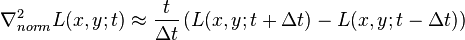In the computer vision literature, this approach is referred to as the Difference of Gaussians (DoG) approach. Besides minor technicalities, however, this operator is in essence similar to the Laplacian and can be seen as an approximation of the Laplacian operator. In a similar fashion as for the Laplacian blob detector, blobs can be detected from scale-space extrema of differences of Gaussians -- see Lindeberg (2012) for the explicit relation between the difference-of-Gaussian operator and the scale-normalized Laplacian operator.
Read more about this topic: Blob Detection
Famous quotes containing the words difference and/or approach:
“What difference is there, do you think, between those in Plato’s cave who can only marvel at the shadows and images of various objects, provided they are content and don’t know what they miss, and the philosopher who has emerged from the cave and sees the real things?”
—Desiderius Erasmus (c. 1466–1536)
“... the ordinary is simply the universal observed from the surface, that the direct approach to reality is not without, but within. Touch life anywhere ... and you will touch universality wherever you touch the earth.”
—Ellen Glasgow (1873–1945)