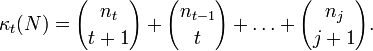Blancmange Curve - Relation To Simplicial Complexes

Relation To Simplicial Complexes

Let

$N=\binom{n_t}{t}+\binom{n_{t-1}}{t-1}+\ldots+\binom{n_j}{j},\quad n_t > n_{t-1} > \ldots > n_j \geq j\geq 1.$

Define the Kruskal–Katona function

$\kappa_t(N)={n_t \choose t+1} + {n_{t-1} \choose t} + \dots + {n_j \choose j+1}.$

The Kruskal–Katona theorem states that this is the minimum number of (t − 1)-simplexes that are faces of a set of N t-simplexes.

As t and N approach infinity, (suitably normalized) approaches the blancmange curve.

Read more about this topic: Blancmange Curve

Famous quotes containing the words relation to and/or relation:

“Hesitation increases in relation to risk in equal proportion to age.”
—Ernest Hemingway (1899–1961)

“When needs and means become abstract in quality, abstraction is also a character of the reciprocal relation of individuals to one another. This abstract character, universality, is the character of being recognized and is the moment which makes concrete, i.e. social, the isolated and abstract needs and their ways and means of satisfaction.”
—Georg Wilhelm Friedrich Hegel (1770–1831)