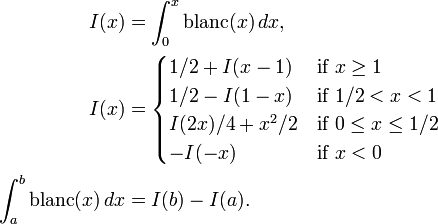Blancmange Curve - Integrating The Blancmange Curve

Integrating The Blancmange Curve

Given that the integral of from 0 to 1 is 1/2, the identity allows the integral over any interval to be computed by the following relation. The computation is recursive with computing time on the order of log of the accuracy required.

$\begin{align} I(x) &= \int_0^x{\rm blanc}(x)\,dx,\\ I(x) &=\begin{cases} 1/2+I(x-1) & \text{if }x \geq 1\\ 1/2-I(1-x) & \text{if }1/2 < x < 1 \\ I(2x)/4+x^2/2 & \text{if } 0 \leq x \leq 1/2 \\ -I(-x) & \text{if } x < 0 \end{cases} \\ \int_a^b{\rm blanc}(x)\,dx &= I(b) - I(a). \end{align}$

Read more about this topic: Blancmange Curve

Famous quotes containing the word curve:

“I have been photographing our toilet, that glossy enameled receptacle of extraordinary beauty.... Here was every sensuous curve of the “human figure divine” but minus the imperfections. Never did the Greeks reach a more significant consummation to their culture, and it somehow reminded me, in the glory of its chaste convulsions and in its swelling, sweeping, forward movement of finely progressing contours, of the Victory of Samothrace.”
—Edward Weston (1886–1958)