BKL Singularity - General Solution With Small Oscillations

General Solution With Small Oscillations

In the above models, metric evolution near the singularity is studied on the example of homogeneous space metrics. It is clear from the characteristic of this evolution that the analytic construction of the general solution for a singularity of such type should be made separately for each of the basic evolution components: for the Kasner epochs, for the process of transitions between epochs caused by "perturbations", for long eras with two perturbations acting simultaneously. During a Kasner epoch (i.e. at small perturbations), the metric is given by eq. 7 without the condition λ = 0.

BKL further developed a matter distribution-independent model (homogeneous or non-homogeneous) for long era with small oscillations. The time dependence of this solution turns out to be very similar to that in the particular case of homogeneous models; the latter can be obtained from the distribution-independent model by a special choice of the arbitrary functions contained in it.

It is convenient, however, to construct the general solution in a system of coordinates somewhat different from synchronous reference frame: g_0α = 0 as in the synchronous frame, but instead of g₀₀ = 1 it is now g₀₀ = −g₃₃. Defining again the space metric tensor γ_αβ = −g_αβ one has, therefore

(eq. 91)

The special space coordinate is written as x3 = z and the time coordinate is written as x0 = ξ (as different from proper time t); it will be shown that ξ corresponds to the same variable defined in homogeneous models. Differentiation by ξ and z is designated, respectively, by dot and prime. Latin indices a, b, c take values 1, 2, corresponding to space coordinates x1, x2 which will be also written as x, y. Therefore, the metric is

(eq. 92)

The required solution should satisfy the inequalities

(eq. 93)

(eq. 94)

(these conditions specify that one of the functions a2, b2, c2 is small compared to the other two which was also the case with homogeneous models).

Inequality eq. 94 means that components γ_a3 are small in the sense that at any ratio of the shifts dxa and dz, terms with products dxadz can be omitted in the square of the spatial length element dl2. Therefore, the first approximation to a solution is a metric eq. 92 with γ_a3 = 0:

(eq. 95)

One can be easily convinced by calculating the Ricci tensor components, using metric eq. 95 and the condition eq. 93 that all terms containing derivatives by coordinates xa are small compared to terms with derivatives by ξ and z (their ratio is ~ γ₃₃ / γ_ab). In other words, to obtain the equations of the main approximation, γ₃₃ and γ_ab in eq. 95 should be differentiated as if they do not depend on xa. Designating

(eq. 96)

one obtains the following equations:

(eq. 97)

(eq. 98)

(eq. 99)

Index raising and lowering is done here with the help of γ_ab. The quantities and λ are the contractions and whereby

(eq. 100)

As to the Ricci tensor components, by this calculation they are identically zero. In the next approximation (i.e., with account to small γ_a3 and derivatives by x, y), they determine the quantities γ_a3 by already known γ₃₃ and γ_ab.

Contraction of eq. 97 gives, and, hence,

(eq. 101)

Different cases are possible depending on the G variable. In the above case g00 = γ33 γab and . The case N > 0 (quantity N is time-like) leads to time singularities of interest. Substituting in eq. 101 f₁ = 1/2 ( ξ + z ) sin y, f₂ = 1/2 ( ξ − z ) sin y results in G of type

(eq. 102)

This choice does not diminish the generality of conclusions; it can be shown that generality is possible (in the first approximation) just on account of the remaining permissible transformations of variables. At N < 0 (quantity N is space-like) one can substitute G = z which generalizes the well-known Einstein–Rosen metric. At N = 0 one arrives at the Robinson–Bondi wave metric that depends only on ξ + z or only on ξ − z (cf.). The factor sin y in eq. 102 is put for convenient comparison with homogeneous models. Taking into account eq. 102, equations 97–99 become

(eq. 103)

(eq. 104)

(eq. 105)

The principal equations are eq. 103 defining the γ_ab components; then, function ψ is found by a simple integration of eqs. 104–105.

The variable ξ runs through the values from 0 to ∞. The solution of eq. 103 is considered at two boundaries, ξ 1 and 1. At large ξ values, one can look for a solution that takes the form of a 1 / √ξ decomposition:

(eq. 106)

whereby

(eq. 107)

(equation 107 needs condition 102 to be true). Substituting eq. 103 in eq. 106, one obtains in the first order

(eq. 108)

where quantities aac constitute a matrix that is inverse to matrix a_ac. The solution of eq. 108 has the form

(eq. 109)

(eq. 110)

where l_a, m_a, ρ, are arbitrary functions of coordinates x, y bound by condition eq. 110 derived from eq. 107.

To find higher terms of this decomposition, it is convenient to write the matrix of required quantities γ_ab in the form

(eq. 111)

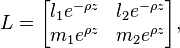
(eq. 112)

where the symbol ~ means matrix transposition. Matrix H is symmetric and its trace is zero. Presentation eq. 111 ensures symmetry of γ_ab and fulfillment of condition eq. 102. If exp H is substituted with 1, one obtains from eq. 111 γ_ab = ξa_ab with a_ab from eq. 109. In other words, the first term of γ_ab decomposition corresponds to H = 0; higher terms are obtained by powers decomposition of matrix H whose components are considered small.

The independent components of matrix H are written as σ and φ so that

(eq. 113)

Substituting eq. 111 in eq. 103 and leaving only terms linear by H, one derives for σ and φ

(eq. 114)

If one tries to find a solution to these equations as Fourier series by the z coordinate, then for the series coefficients, as functions of ξ, one obtains Bessel equations. The major asymptotic terms of the solution at large ξ are

(eq. 115)

Coefficients A and B are arbitrary complex functions of coordinates x, y and satisfy the necessary conditions for real σ and φ; the base frequency ω is an arbitrary real function of x, y. Now from eqs. 104–105 it is easy to obtain the first term of the function ψ:

(eq. 116)

(this term vanishes if ρ = 0; in this case the major term is the one linear for ξ from the decomposition: ψ = ξq (x, y) where q is a positive function).

Therefore, at large ξ values, the components of the metric tensor γ_ab oscillate upon decreasing ξ on the background of a slow decrease caused by the decreasing ξ factor in eq. 111. The component γ₃₃ = eψ decreases quickly by a law close to exp (ρ2ξ2); this makes it possible for condition eq. 93.

Next BKL consider the case ξ 1. The first approximation to a solution of eq. 103 is found by the assumption (confirmed by the result) that in these equations terms with derivatives by coordinates can be left out:

(eq. 117)

This equation together with the condition eq. 102 gives

(eq. 118)

where λ_a, μ_a, s₁, s₂ are arbitrary functions of all 3 coordinates x, y, z, which are related with other conditions

(eq. 119)

Equations 104–105 give now

(eq. 120)

The derivatives, calculated by eq. 118, contain terms ~ ξ4s₁ − 2 and ~ ξ4s₂ − 2 while terms left in eq. 117 are ~ ξ−2. Therefore, application of eq. 103 instead of eq. 117 is permitted on conditions s₁ > 0, s₂ > 0; hence 1 − > 0.

Thus, at small ξ oscillations of functions γ_ab cease while function γ₃₃ begins to increase at decreasing ξ. This is a Kasner mode and when γ₃₃ is compared to γ_ab, the above approximation is not applicable.

In order to check the compatibility of this analysis, BKL studied the equations = 0, = 0, and, calculating from them the components γ_a3, confirmed that the inequality eq. 94 takes place. This study showed that in both asymptotic regions the components γ_a3 were ~ γ₃₃. Therefore, correctness of inequality eq. 93 immediately implies correctness of inequality eq. 94.

This solution contains, as it should be for the general case of a field in vacuum, four arbitrary functions of the three space coordinates x, y, z. In the region ξ 1 these functions are, e.g., λ₁, λ₂, μ₁, s₁. In the region ξ 1 the four functions are defined by the Fourier series by coordinate z from eq. 115 with coefficients that are functions of x, y; although Fourier series decomposition (or integral?) characterizes a special class of functions, this class is large enough to encompass any finite subset of the set of all possible initial conditions.

The solution contains also a number of other arbitrary functions of the coordinates x, y. Such two-dimensional arbitrary functions appear, generally speaking, because the relationships between three-dimensional functions in the solutions of the Einstein equations are differential (and not algebraic), leaving aside the deeper problem about the geometric meaning of these functions. BKL did not calculate the number of independent two-dimensional functions because in this case it is hard to make unambiguous conclusions since the three-dimensional functions are defined by a set of two-dimensional functions (cf. for more details).

Finally, BKL go on to show that the general solution contains the particular solution obtained above for homogeneous models.

Substituting the basis vectors for Bianchi Type IX homogeneous space in eq. 7 the space-time metric of this model takes the form

(eq. 121)

When c2 a2, b2, one can ignore c2 everywhere except in the term c2 dz2. To move from the synchronous frame used in eq. 121 to a frame with conditions eq. 91, the transformation dt = c dξ/2 and substitution z → z/2 are done. Assuming also that χ ≡ ln (a/b) 1, one obtains from eq. 121 in the first approximation:

(eq. 122)

Similarly, with the basis vectors of Bianchi Type VIII homogeneous space, one obtains

(eq. 123)

According to the analysis of homogeneous spaces above, in both cases ab = ξ (simplifying = ξ₀) and χ is from eq. 51; function c (ξ) is given by formulae eq. 53 and eq. 61, respectively, for models of Types IX and VIII.

Identical metric for Type VIII is obtained from eqs. 112, 115, 116 choosing two-dimensional vectors l_a and m_a in the form

(eq. 124)

and substituting

(eq. 125)

To obtain the metric for Type IX, one should substitute

(eq. 126)

(for calculation of c (ξ) the approximation in eq. 116 is not sufficient and the term in ψ linear by ξ is calculated)

This analysis was done for empty space. Including matter does not make the solution less general and does not change its qualitative characteristics.