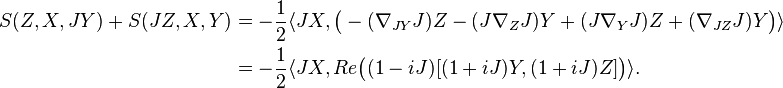Bismut Connection

In mathematics, the Bismut connection is the unique connection on a complex manifold that satisfies the following conditions,

  1. It preserves the metric
  2. It preserves the complex structure
  3. The torsion contracted with the metric, i.e., is totally skew-symmetric.

Bismut has used this connection when proving a local index formula for the Dolbeault operator on non-Kähler manifolds. Bismut connection has applications in type II and heterotic string theory.

The explicit construction goes as follows. Let denote the pairng of two vectors using the metric that is Hermitian w.r.t the complex structure, i.e. . Further let be the Levi-Civita connection. Define first a tensor such that . It is easy to see that this tensor is anti-symmetric in the first and last entry, i.e. the new connection still preserves the metric. In concrete terms, the new connection is given by with being the Levi-Civita connection. It is also easy to see that the new connection preserves the complex structure. However, the tensor is not yet totall anti-symmetric, in fact the anti-symmetrization will lead to the Nijenhuis tensor. Denote the anti-symmetrization as, with given explicitly as

We show that still preserves the complex structure (that it preserves the metric is easy to see), i.e. .

\begin{align} S(Z,X,JY)+S(JZ,X,Y)&=-\frac12\langle JX, \big(-(\nabla_{JY}J)Z-(J\nabla_ZJ)Y+(J\nabla_YJ)Z+(\nabla_{JZ}J)Y\big)\rangle\\ &=-\frac12\langle JX, Re\big((1-iJ)\big)\rangle.\end{align}

So if is integrable, then above term vanishes, and the connection

gives the Bismut connection.


Famous quotes containing the word connection:

    “The connection between our knowledge and the abyss of being is still real, and the explication must be not less magnificent.”
    —Ralph Waldo Emerson (1803–1882)