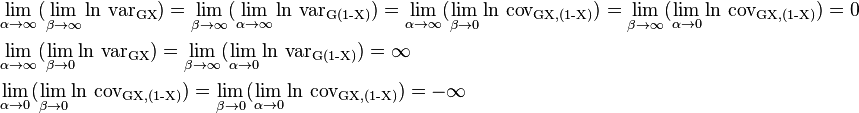Beta Distribution - Properties - Measures of Statistical Dispersion - Geometric Variance and Covariance

Geometric Variance and Covariance

The logarithm of the geometric variance of a distribution with random variable X is the second moment of the logarithm of X centered around the geometric mean of X, :

$\begin{align} \ln \,\operatorname{var_{GX}} &= \operatorname{E} \\ &= \operatorname{E})^2] \\ &= \operatorname{E} - (\operatorname{E})^2\\ &= \operatorname{var} \end{align}$

and therefore, the geometric variance is:

In the Fisher information matrix, and the curvature of the log likelihood function, the logarithm of the geometric variance of the reflected variable (1-X) and the logarithm of the geometric covariance between X and (1-X) appear:

$\begin{align} \ln \,\operatorname{var_{G(1-X)}} &= \operatorname{E} \\ &= \operatorname{E})^2] \\ &= \operatorname{E} - (\operatorname{E})^2\\ &= \operatorname{var} \end{align}$

$\begin{align} \ln \,\operatorname{cov_{G{X,(1-X)}}} &= \operatorname{E} \\ &= \operatorname{E})(\ln (1-X) - \operatorname{E})] \\ &= \operatorname{E}\big - \operatorname{E}\operatorname{E}\\ &= \operatorname{cov} \end{align}$

For a beta distribution, higher order logarithmic moments can be derived by using the representation of a beta distribution as a proportion of two Gamma distributions and differentiating through the integral. They can be expressed in terms of higher order poly-gamma functions. See the section titled "Other moments, Moments of transformed random variables, Moments of logarithmically-transformed random variables". The variance of the logarithmic variables and covariance of lnX and ln(1-X) are:

where the trigamma function, denoted, is the second of the polygamma functions, and is defined as the derivative of the digamma function: .

Therefore,

The accompanying plots show the log geometric variances and log geometric covariance versus the shape parameters α and β. The plots show that the log geometric variances and log geometric covariance are close to zero for shape parameters α and β greater than 2, and that the log geometric variances rapidly rise in value for shape parameter values α and β less than unity. The log geometric variances are positive for all values of the shape parameters. The log geometric covariance is negative for all values of the shape parameters, and it reaches large negative values for α and β less than unity.

Following are the limits with one parameter finite (non zero) and the other approaching these limits:

$\begin{align} &\lim_{\alpha\to 0} \ln \,\operatorname{var_{GX}} = \lim_{\beta\to 0} \ln \,\operatorname{var_{G(1-X)}} =\infty \\ &\lim_{\beta \to 0} \ln \,\operatorname{var_{GX}} = \lim_{\alpha \to \infty} \ln \,\operatorname{var_{GX}} = \lim_{\alpha \to 0} \ln \,\operatorname{var_{G(1-X)}} = \lim_{\beta\to \infty} \ln \,\operatorname{var_{G(1-X)}} = \lim_{\alpha\to \infty} \ln \,\operatorname{cov_{G{X,(1-X)}}} = \lim_{\beta\to \infty} \ln \,\operatorname{cov_{G{X,(1-X)}}} = 0\\ &\lim_{\beta \to \infty} \ln \,\operatorname{var_{GX}} = \psi_1(\alpha)\\ &\lim_{\alpha\to \infty} \ln \,\operatorname{var_{G(1-X)}} = \psi_1(\beta)\\ &\lim_{\alpha\to 0} \ln \,\operatorname{cov_{G{X,(1-X)}}} = - \psi_1(\beta)\\ &\lim_{\beta\to 0} \ln \,\operatorname{cov_{G{X,(1-X)}}} = - \psi_1(\alpha)\\ \end{align}$

Limits with two parameters varying:

$\begin{align} &\lim_{\alpha\to \infty}( \lim_{\beta \to \infty} \ln \,\operatorname{var_{GX}}) = \lim_{\beta \to \infty}( \lim_{\alpha\to \infty} \ln \,\operatorname{var_{G(1-X)}}) = \lim_{\alpha\to \infty} (\lim_{\beta \to 0} \ln \,\operatorname{cov_{G{X,(1-X)}}}) = \lim_{\beta\to \infty}( \lim_{\alpha\to 0} \ln \,\operatorname{cov_{G{X,(1-X)}}}) =0\\ &\lim_{\alpha\to \infty} (\lim_{\beta \to 0} \ln \,\operatorname{var_{GX}}) = \lim_{\beta\to \infty} (\lim_{\alpha\to 0} \ln \,\operatorname{var_{G(1-X)}}) = \infty\\ &\lim_{\alpha\to 0} (\lim_{\beta \to 0} \ln \,\operatorname{cov_{G{X,(1-X)}}}) = \lim_{\beta\to 0} (\lim_{\alpha\to 0} \ln \,\operatorname{cov_{G{X,(1-X)}}}) = - \infty \end{align}$

Although both and are asymmetric, in the case that both shape parameters are equal, the log geometric variances are equal: . This equality follows from the following symmetry displayed between both log geometric variances: . The log geometric covariance is symmetric:

Read more about this topic: Beta Distribution, Properties, Measures of Statistical Dispersion

Famous quotes containing the words geometric and/or variance:

“New York ... is a city of geometric heights, a petrified desert of grids and lattices, an inferno of greenish abstraction under a flat sky, a real Metropolis from which man is absent by his very accumulation.”
—Roland Barthes (1915–1980)

“There is an untroubled harmony in everything, a full consonance in nature; only in our illusory freedom do we feel at variance with it.”
—Fyodor Tyutchev (1803–1873)