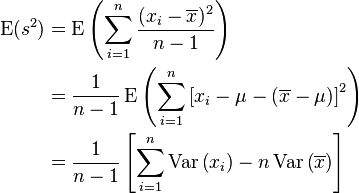Bessel's Correction - Alternate Proof of Correctness

Alternate Proof of Correctness

Click to expand

Recycling an identity for variance,

\begin{align} \sum_{i=1}^n \left(x_i - \overline{x} \right)^2 &= \sum_{i=1}^n \left(x_i - \frac 1 n \sum_{j=1}^n x_j \right)^2 \\ &= \sum_{i=1}^n x_i^2 - n \left(\frac 1 n \sum_{j=1}^n x_j \right)^2 \\ &= \sum_{i=1}^n x_i^2 - n \overline{x}^2 \end{align}

so

\begin{align} \operatorname{E}\left(\sum_{i=1}^n \left^2 \right) &= \operatorname{E}\left(\sum_{i=1}^n (x_i-\mu)^2 - n (\overline{x}-\mu)^2 \right) \\ &= \sum_{i=1}^n \operatorname{E}\left((x_i-\mu)^2 \right) - n \operatorname{E}\left((\overline{x}-\mu)^2\right) \\ &= \sum_{i=1}^n \operatorname{Var}\left(x_i \right) - n \operatorname{Var}\left(\overline{x} \right) \end{align}

and by definition,

\begin{align} \operatorname{E}(s^2) & = \operatorname{E}\left(\sum_{i=1}^n \frac{(x_i-\overline{x})^2}{n-1} \right)\\ & = \frac{1}{n-1} \operatorname{E}\left(\sum_{i=1}^n \left^2 \right)\\ &= \frac{1}{n-1} \left \end{align}

Note that, since x1, x2, · · ·, xn are a random sample from a distribution with variance σ2, it follows that for each i = 1, 2, . . ., n:

and also

This is a property of the variance of uncorrelated variables, arising from the Bienaymé formula. The required result is then obtained by substituting these two formulae:

\operatorname{E}(s^2) = \frac{1}{n-1}\left = \frac{1}{n-1}(n\sigma^2-\sigma^2) = \sigma^2. \,


Read more about this topic:  Bessel's Correction

Famous quotes containing the words alternate, proof and/or correctness:

    “Germany is a queer country: one can’t regard it dispassionately. I alternate between hating it thoroughly, stick, stock and stone, and yearning over it fit to break my heart. I can’t help feeling it a young and adorable country—adolescent—with the faults of adolescence.”
    —D.H. (David Herbert)

    “A short letter to a distant friend is, in my opinion, an insult like that of a slight bow or cursory salutation—a proof of unwillingness to do much, even where there is a necessity of doing something.”
    —Samuel Johnson (1709–1784)

    “What will happen once the authentic mass man takes over, we do not know yet, although it may be a fair guess that he will have more in common with the meticulous, calculated correctness of Himmler than with the hysterical fanaticism of Hitler, will more resemble the stubborn dullness of Molotov than the sensual vindictive cruelty of Stalin.”
    —Hannah Arendt (1906–1975)