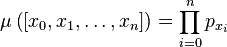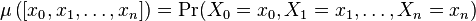Bernoulli Scheme - Definition

Definition

A Bernoulli scheme is a discrete-time stochastic process where each independent random variable may take on one of N distinct possible values, with the outcome i occurring with probability, with i = 1, ..., N, and

The sample space is usually denoted as

as a short-hand for

X=\{ x=(\ldots,x_{-1},x_0,x_1,\ldots) : x_k \in \{1,\ldots,N\} \; \forall k \in \mathbb{Z} \}.

The associated measure is called the Bernoulli measure

The σ-algebra on X is the product sigma algebra; that is, it is the (countable) direct product of the σ-algebras of the finite set {1, ..., N}. Thus, the triplet

is a measure space. The elements of are commonly called cylinder sets. Given a cylinder set, its measure is

\mu\left(\right)= \prod_{i=0}^n p_{x_i}

The equivalent expression, using the notation of probability theory, is

\mu\left(\right)= \mathrm{Pr}(X_0=x_0, X_1=x_1, \ldots, X_n=x_n)

for the random variables

The Bernoulli scheme, as any stochastic process, may be viewed as a dynamical system by endowing it with the shift operator T where

Since the outcomes are independent, the shift preserves the measure, and thus T is a measure-preserving transformation. The quadruplet

is a measure-preserving dynamical system, and is called a Bernoulli scheme or a Bernoulli shift. It is often denoted by

The N = 2 Bernoulli scheme is called a Bernoulli process. The Bernoulli shift can be understood as a special case of the Markov shift, where all entries in the adjacency matrix are one, the corresponding graph thus being a clique.

Read more about this topic:  Bernoulli Scheme

Famous quotes containing the word definition:

    “One definition of man is “an intelligence served by organs.””
    —Ralph Waldo Emerson (1803–1882)

    “The very definition of the real becomes: that of which it is possible to give an equivalent reproduction.... The real is not only what can be reproduced, but that which is always already reproduced. The hyperreal.”
    —Jean Baudrillard (b. 1929)

    “Was man made stupid to see his own stupidity?
    Is God by definition indifferent, beyond us all?
    Is the eternal truth man’s fighting soul
    Wherein the Beast ravens in its own avidity?”
    —Richard Eberhart (b. 1904)