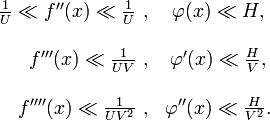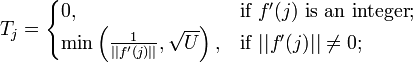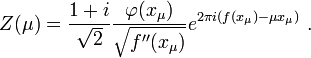ATS Theorem - ATS Theorem

ATS Theorem

Let the real functions ƒ(x) and satisfy on the segment the following conditions:

1) and are continuous;

2) there exist numbers and such that

and

$\begin{array}{rc} \frac{1}{U} \ll f''(x) \ll \frac{1}{U} \ ,& \varphi(x) \ll H ,\\ \\ f'''(x) \ll \frac{1}{UV} \ ,& \varphi'(x) \ll \frac{H}{V} ,\\ \\ f''''(x) \ll \frac{1}{UV^2} \ ,& \varphi''(x) \ll \frac{H}{V^2} . \\ \\ \end{array}$

Then, if we define the numbers from the equation

$f'(x_\mu) = \mu,$

we have

$\sum_{a< \mu\le b} \varphi(\mu)e^{2\pi i f(\mu)} = \sum_{f'(a)\le\mu\le f'(b)}C(\mu)Z(\mu) + R ,$

where

$R = O \left(\frac{HU}{b-a} + HT_a + HT_b + H\log\left(f'(b)-f'(a)+2\right)\right);$

$T_j = \begin{cases} 0, & \text{if } f'(j) \text{ is an integer}; \\ \min\left(\frac{1}{||f'(j)||}, \sqrt{U}\right), & \text{if } ||f'(j)|| \ne 0; \\ \end{cases}$

$C(\mu) = \begin{cases} 1, & \text{if } f'(a) < \mu < f'(b) ; \\ \frac{1}{2},& \text{if } \mu = f'(a)\text{ or }\mu = f'(b) ;\\ \end{cases}$

$Z(\mu) = \frac{1+i}{\sqrt 2}\frac{\varphi(x_{\mu})}{\sqrt{f''(x_{\mu})}} e^{2\pi i(f(x_{\mu})- \mu x_{\mu})} \ .$

The most simple variant of the formulated theorem is the statement, which is called in the literature the Van der Corput lemma.

Famous quotes containing the word theorem:

“To insure the adoration of a theorem for any length of time, faith is not enough, a police force is needed as well.”
—Albert Camus (1913–1960)