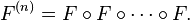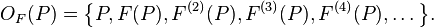Definitions and Notation From Discrete Dynamics
Let S be a set and let F : S → S be a map from S to itself. The iterate of F with itself n times is denoted
A point P ∈ S is periodic if F(n)(P) = P for some n > 1.
The point is preperiodic if F(k)(P) is periodic for some k ≥ 1.
The (forward) orbit of P is the set
Thus P is preperiodic if and only if its orbit OF(P) is finite.
Read more about this topic: Arithmetic Dynamics
Famous quotes containing the words definitions, discrete and/or dynamics:
“What I do not like about our definitions of genius is that there is in them nothing of the day of judgment, nothing of resounding through eternity and nothing of the footsteps of the Almighty.”
—G.C. (Georg Christoph)
“The mastery of one’s phonemes may be compared to the violinist’s mastery of fingering. The violin string lends itself to a continuous gradation of tones, but the musician learns the discrete intervals at which to stop the string in order to play the conventional notes. We sound our phonemes like poor violinists, approximating each time to a fancied norm, and we receive our neighbor’s renderings indulgently, mentally rectifying the more glaring inaccuracies.”
—W.V. Quine (b. 1908)
“Anytime we react to behavior in our children that we dislike in ourselves, we need to proceed with extreme caution. The dynamics of everyday family life also have a way of repeating themselves.”
—Cathy Rindner Tempelsman (20th century)